Un grande scienziato cattolico: Louis Augustin Cauchy
Lezione tenuta dal dott. Nicola Binaghi il 27 aprile 2000
Nicola Binaghi
I luoghi comuni della propaganda anticattolica:
“La Chiesa soffoca l’indagine scientifica e si oppone al progresso”
L’esempio di un grande scienziato cattolico: Louis Augustin Cauchy
Nell’ambito di una serie di incontri atti a smentire l’affermazione secondo la quale la Chiesa ostacolerebbe il progresso scientifico, presenteremo la figura di un grande scienziato cattolico, il matematico Augustin Louis Cauchy.

Una sua affermazione del 1842 riassume il programma della sua vita di uomo e di scienziato:
“ La verità è un tesoro inestimabile che, quando riusciamo ad acquisirla, non può portarci rimorso o dolore; non può rendere inquieta o insoddisfatta la nostra anima. Il solo pensiero dei suoi attributi celesti, della sua bellezza divina è sufficiente per ripagarci di tutti i sacrifici che possiamo avere fatto per scoprirla. In realtà, la gioia stessa del paradiso non è nient’altro che il pieno e completo possesso della verità”
In questo incontro intendiamo rendere testimonianza ad un grande scienziato, al tempo stesso un semplice laico cattolico che prese molto sul serio i comandamenti sia nella vita privata che in quella pubblica, una persona che fece fruttare al meglio i talenti ricevuti. Una persona reale, con i suoi pregi ed i suoi difetti, ma certamente un uomo che ha lasciato un segno indelebile nella storia della scienza.
Premessa
I grandi scienziati che vissero integralmente la fede cattolica costituiscono la più importante testimonianza dell’inscindibile legame tra Fede Cristiana e progresso scientifico. La loro vita e le loro opere provano l’impossibilità del secondo senza la prima. Come ha brillantemente mostrato l’amico dott. Luciano Benassi nei suoi interventi a questa scuola di qualche anno fa, è infatti soltanto grazie al radicarsi del Cristianesimo ed alla sua visione unitaria del creato che l’indagine scientifica può assumere quel carattere di organicità che è indispensabile per la corretta comprensione dei fenomeni naturali, è soltanto col Cristianesimo e quindi in Occidente, in Europa, che si può parlare di “Scienza”, intesa come unità organica del sapere, che è invece sconosciuta al mondo antico. Se la scienza e la tecnologia sono prova della benevolenza e della grazia di Dio verso l’umanità, gli uomini che in virtù della propria fede contribuirono in modo sostanziale allo sviluppo scientifico sono da riguardare come strumenti della Provvidenza, che li scelse come mezzi per tale fine. Ed anche come risposte viventi ad una pretesa quanto pretestuosa inconciliabilità tra fede Cristiana, soprattutto Cattolica, e progresso scientifico. Al contrario di quanto normalmente si crede in virtù della vulgata scientista dominante, nella storia dell’umanità sono veramente numerosi gli uomini che, vivendo integralmente la propria fede, si segnalarono nel campo della scienza. Per la sua attualità, spicca il nome di uno dei più grandi matematici forse, assieme a J. C. Gauss (1777-1855), il più grande dell’epoca moderna: Augustin Louis Cauchy (n. a Parigi, 21-Agosto-1789, m. a Sceaux, 23-Maggio-1857).
Cauchy lavorò incessantemente per opporsi e per mettere riparo ai dolorosi risultati della Rivoluzione dell’89. La considerò un disastro totale e ne combatté sempre le idee. Egli va considerato il più grande ed il più fedele portavoce della Contro-Rivoluzione Cattolica e Monarchica nel mondo scientifico e accademico della Francia del suo tempo.
Questo breve intervento si articola in tre parti:
- Alcuni cenni biografici
- Uno sguardo alla produzione scientifica
- Alcuni cenni all’impegno sociale
Augustin Louis Cauchy nasce a Parigi il 21 Agosto 1789, primogenito di sei figli. Il padre Louis François, coltissimo giurista parlamentare, cattolico e monarchico, primo aiutante del Luogotenente generale della polizia di Parigi, per sfuggire alle persecuzioni della Rivoluzione Francese è costretto a trasferirsi con la famiglia nella casa di Arcueil (al proposito, il Bell, autore della più famosa e diffusa biografia di grandi matematici, benché di taglio illuminista-razionalista e non certo favorevole – basti pensare che il suo articolo su Cauchy si intitola “Matematica e mulini a vento”, dove per mulini a vento si intendono la fede cattolica e la fedeltà legittimista -, commenta “Dio solo sa come sfuggì alla ghigliottina […]” ), dove sopravvive fra grandissimi stenti, tanto che lo stesso fisico di Augustin Louis ne risulta assai indebolito (in altre parole, stentavano ad avere qualcosa da mangiare). Ecco come lo stesso Cauchy descrive la situazione: “Non avevamo mai più di mezza oncia di pane, e qualche volta nemmeno quella. A questa carenza supplivamo con la piccola dose di dure gallette e di riso che ci era concessa“.
Il padre provvede personalmente, poiché le scuole erano state chiuse dai rivoluzionari o comunque non era consigliabile frequentarle (…), all’istruzione e all’educazione religiosa dei figli, sicché Augustin Louis diviene esperto in lettere, tanto da comporre versi poetici sia in latino che in francese.
Dopo avere contratto e superato il vaiolo e vissuto per anni sotto la continua minaccia di arresto del padre, alla caduta di Robespierre (27 Luglio 1794), la famiglia Cauchy fa ritorno a Parigi.
La sua propensione per la matematica viene scoperta da un vicino di casa, Pierre Simone de Laplace (1749-1827), matematico e fisico famoso ed affermato, e dal torinese Giuseppe Luigi Lagrange (1736-1813), anch’egli famoso analista e meccanico, che ebbe a dire: “Lo vedete? ebbene, vi dico che come matematico ci soppianterà tutti“.
Nel 1802 entra, alla Scuola Centrale del Pantheon, dove si distingue particolarmente in greco ed in latino, scrivendo anche componimenti in versi che vincono svariati premi. Nel 1804 lascia la scuola e riceve la prima Comunione (questo evento va ricordato perché, nell'”economia generale” del personaggio, è un evento importantissimo, che egli stesso ricorda come tale ed al quale si preparò con molta serietà).
Nel 1805, a soli sedici anni, entra all’Ecole Polytechnique noto “covo” di rivoluzionari ed illuministi, contrariamente alla tradizione famigliare, che vedeva i suoi fratelli, sulle orme del padre, compiere studi di legge. Risulterà sempre fra i primi, nonostante abbia vita assai difficile a causa del clima anticlericale imperante (“i suoi compagni non gli davano pace e lo prendevano in giro per le su pratiche religiose, ma Cauchy riuscì sempre a padroneggiarsi e cercò perfino di convertire alcuni dei suoi tormentatori“). Il suo tutore principale alla Ecole Polytecnique sarà Ampere (il grande fisico dell’elettricità).Uno degli assistenti tutori in analisi e meccanica è Paul-Emile Teysseyre, profondamente cattolico e membro della Congregazione della Santa Vergine (Congregation de la Saint Vierge), fondata nel 1801 dal gesuita padre Jean-Baptiste Bourdier Delpuis, allo scopo di riunire i giovani di buona famiglia in preghiera comunitaria e unirli contro le minacce rappresentate dalla mancanza di fede, miscredenza, irreligione e secolarismo di quei tempi. Lo scopo della congregazione, il cui motto era cor unum et anima una era quello di formare una elite di giovani cattolici che andasse ad occupare posti influenti nel mondo della scienza e della politica, al fine di ricostruire l’intelaiatura cattolica della società, assolutamente perduta e caduta in mani nemiche con il secolo dei lumi e la Rivoluzione. Cauchy entrerà a far parte dell’associazione, che tentava di infiltrarsi nelle fila della Ecole Polytecnique, nel 1808, subito dopo avere concluso la sua esperienza alla scuola. Con lui, entrerà anche il suo amico e futuro famoso matematico Jacques Binet (si ricorda il teorema di Binet: il determinante del prodotto di due matrici è uguale al prodotto dei determinanti delle due matrici ), precedentemente ateo. Torneremo più avanti sull’argomento.
Pian piano, la Congregazione mostrerà sempre più apertamente il suo aspetto cattolico sociale legittimista, contrario al governo napoleonico ed incontrerà sempre più forte il sospetto e l’avversità del regime, che ne sospenderà gli incontri e l’attività pubblica fino al 1813 (in quell’anno Cauchy, al rientro da Cherbourg, potrà riprendere a frequentare le riunioni)
Nel 1807 entra alla scuola degli ingegneri civili (Ecole des Ponts et Chausses) e, nonostante i suoi soli diciassette anni, si mostra subito superiore ai suoi compagni ventenni che già frequentano la scuola da due anni. Oltre alla frequentazione dei normali corsi di ingegneria, si dedica all studio dell’inglese, del tedesco e dell’italiano (più tardi, attorno agli anni 40, studierà anche l’ebraico per poter leggere le Scritture in lingua originale).
Terminata la scuola di ingegneria a soli 21 anni, nonostante la sua fama di monarchico legittimista, dal governo napoleonico gli viene affidato un incarico di ingegnere militare a Cherbourg.Porta con sé tre soli libri, due dei quali di matematica (la Meccanica celeste di Laplace e il Trattato delle funzioni analitiche di Lagrange), mentre il terzo è l’Imitazione di Gesù Cristo.
Mentre lavora, e duramente (“Mi alzo ogni giorno alle quattro del mattino e sono occupato da quel momento in poi…. Non mi stanco del lavoro: al contrario, mi rinvigorisce e sono in perfetta salute“) non trascura i doveri di carità, che anzi occupano sempre la prima posizione nella lista delle sue preoccupazioni, pur da militare in guerra. Ecco cosa scrive in una lettera del 3 luglio 1811: ” […] Questo mese, il mio lavoro ordinario è aumentato a causa dell’arrivo dei prigionieri spagnuoli […]. In otto giorni abbiamo dovuto costruire dei baraccamenti e preparare letti da campo per 1200 uomini … Finalmente i nostri prigionieri sono alloggiati e coperti ; hanno letti da campo, paglia, alimenti, e si considerano particolarmente fortunati …“.
Mentre svolge il suo incarico, pubblica i primi lavori, che riguardano i poliedri (dimostrando che gli angoli di un poliedro convesso sono determinati dalle sue facce [S+F=A+P+1, dove P è il numero dei poliedri, F il numero delle facce, A il numero degli spigoli e S quello dei vertici; generalizzazione di una formula di Eulero: S+(F-1)=A+1 che si ottiene ponendo P=1]: per questo suo primo lavoro fu incoraggiato da Legendre (Adrien-Marie Legendre 1752-1833, matematico nato a Tolosa ed insegnante all’Ecole militaire; famoso per i suoi studi sulla teoria dei numeri e sulle funzioni ellittiche, scrisse anche un trattato di geometria elementare che per decine d’anni fu utilizzato come testo nelle scuole medie) e da Malus (Etienne-Louis, Parigi, 1775-1812; matematico e fisico famoso per gli studi di ottica; scopritore del fenomeno della polarizzazione, di cui scrisse ampiamente: legge di Malus & teorema di Malus) e le funzioni simmetriche (il lavoro su queste ultime fu pubblicato dalla Ecole Polytechnique). Malus afferma: “Le prove sono rigorose e dimostrate con estrema eleganza “.
Il 22 Febbraio 1812 viene nominato corrispondente della Societe Philomatique, una prestigiosa appendice dell’Accademia delle Scienze che si occupava di matematica.
Anche nello svolgere il suo incarico di ingegnere militare incontra l’ostilità dell’ambiente anticattolico che lo circonda, che ne disprezza sia la coerenza politica legittimista, sia le pratiche religiose (Cauchy pregava, come è proprio di qualsiasi cristiano degno di questo nome. Non si deve pensare che si dedicasse a pratiche dubbie o straordinarie, semplicemente pregava con regolarità, come era normale per un laico cristiano; ma l’ambiente era talmente anticlericale da non poter tollerare nemmeno questo).
Pur non cedendo mai di un passo quanto alla dottrina ed alla morale, nelle continue discussioni alle quali era costretto, cercherà sempre di mantenere un atteggiamento caritatevole e comprensivo nei confronti di coloro che lo dileggiavano, dimostrando un estremo controllo di sé (nei suoi confronti era in atto una vera e propria persecuzione almeno psicologica, se non fisica; si pensi che arrivarono perfino a scrivere di lui che era pazzo, perché pregava; ecco la sua risposta: “E’ ridicolo pensare che la religione possa far girare la testa ad un uomo, e se tutti i pazzi fossero mandati al manicomio, queste provvidenziali istituzioni ospiterebbero più filosofi (“philosophes”, n.d.r.) che cristiani“. Questa pratica di far passare per pazzo chi professi opinioni politiche e/o religiose diverse da quelle dell’establishment sarà poi ripresa e sviluppata con successo nei paesi del “Socialismo reale” circa un secolo più tardi, ma, come si vede, le basi giacobine erano già state gettate …).
Mentre decide di darsi come programma per il resto della sua vita la ricerca della verità , il troppo lavoro ed il troppo studio (in questo periodo giungerà ad importanti risultati nella teoria dei determinanti) gli provocano uno stato di prostrazione fisico-nervosa che lo spinge a chiedere di essere trasferito a Parigi. La richiesta viene accolta ed il trasferimento diviene effettivo nel 1813: lavorerà alla costruzione del Canaled’Ourcq.
Nel frattempo, mentre ha ormai deciso che la carriera universitaria sarà l’obiettivo della sua vita professionale, sempre a causa delle sue idee contro-rivoluzionarie cattoliche e legittimiste, gli sono più volte precluse cattedre e posizioni universitarie. Ad esempio, un posto di primo piano al Bureau des Longitudes gli verrà rifiutato e gli sarà preferito Poinsot (il fisico-matematico che studiò il moto del punto materiale libero, noto appunto come moto alla Poinsot).
Nel 1814, basandosi sui risultati di Laplace, inizia lo studio dell’Analisi, approfondendo la teoria degli integrali definiti. Nello stesso anno, godendo del favore dello stesso Laplace, da corrispondente diviene membro effettivo della Societè Philomatique, che è l’anticamera dell’Accademia delle Scienze, dove non era riuscito ad entrare perché gli era stato preferito il più anziano Ampere.
Nel luglio 1815 ritorna sul trono Luigi XVIII (1755-1824) ed ha inizio la politica di restaurazione.
In seguito alla radiazione dall’Accademia delle Scienze del rivoluzionario Gaspard Monge (1746-1818; giacobino, già ministro della Marina e poi collaboratore di Napoleone; è l’inventore della geometria descrittiva) ed alla rimozione di Carnot (noto per il famoso teorema sui trinagoli, un po’ meno per essere fra i mandanti del genocidio vandeano), Cauchy, dopo avere pubblicato uno studio sulle onde ed uno studio sui numeri poligonali, (vedi oltre) su indicazione di Lamennais (che al momento era ancora nella sua fase lgittimista/contro-rivoluzionaria) che fa pressioni su Laplace, è nominato ripetitore (cioè assistente) di Analisi alla Ecole Polytecnique, dove i professori erano Ampere e Poinsot (quest’ultimo fu rimosso). Di questo periodo sono gli studi Di Cauchy sulla convergenza delle serie. Ma ciò che lo rese veramente famoso da questo punto in avanti fu la soluzione di uno dei problemi proposti da Fermat sui numeri poligonali (1601-1665, grande geometra e studioso della teoria dei numeri) a Mersenne (1588-1648, frate dell’ordine dei Minimi, amico sia di Fermat che di Descartes) più di un secolo prima ed ancora insoluti: “Ogni intero positivo è la somma di tre numeri triangolari, quattro numeri quadrati, cinque numeri pentagonali, …”.
[I numeri poligonali, detti anche figurati, erano conosciuti fin dall’antichità ed avevano un valore misterico per i pitagorici. Corrispondono a particolari disposizioni di punti all’interno dei poligoni.
I numeri triangolari sonotaliche:N=1+2+3+…+n= n(n+1)/2.Quadrati:1+3+5+7+…+(2n-1).Pentagonali:N=1+4+7+…+(3n-2)= n(3n-1)/2.Esagonali:N=1+5+9+…+(4n-3)=2n2-n].
Nel frattempo, per dare un’idea della situazione storica, è interessante notare che nel 1815 si verifica una rivolta degli studenti liberali-rivoluzionari alla Ecole Polytecnique. Alla testa della rivolta era August Comte, futuro capofila del positivismo. Naturalmente, Cauchy subirà la contestazione degli studenti liberali …
In seguito viene nominato professore di Fisica-Matematica al Collegio di Francia, al posto di Biot, dove tiene un ciclo di lezioni sul calcolo integrale, dando anche la definizione rigorosa di integrale. Infine diviene professore alla Sorbona, dove pubblica una vastissima produzione di opere scientifiche: nessuno prima di lui aveva mai avuto una produzione così feconda. Al contrario di quanto affermava la propaganda liberale, nel tentativo di screditarlo, è invece un fatto che fu sempre pronto a sostenere i giovani di talento, offrendo loro opportunità per affermarsi. Nel 1818, il suo studente Charle Combes dirà di lui: “fummo impressionati dall’eleganza della sua analisi …. Davvero, Cauchy aveva il genio di Eulero, Lagrange, Laplace, Gauss e Jacobi … ”
Il 4 aprile 1818, nella chiesa di S. Sulpicio a Parigi, sposa Aloise de Bure appartenente ad una famiglia di editori (ciò gli permise di pubblicare con facilità un gran numero di opere). In segno di stima ed approvazione, Re Luigi XVIII e tutta la famiglia reale firmano il contratto matrimoniale. Nel 1819 nasce la prima delle due figlie, Marie Francoise Alicia. La seconda, Marie Mathilde, nasce nel 1823.
Nel 1821 pubblica “Analyse Algebrique”, in cui pone le definizioni di limite, di funzione, di continuità e continuità come limite, di infinitesimo e di infinito che segnano la svolta nella direzione del rigore per tutta la matematica moderna. Tra il 1821 ed il 1825 pubblica grandi testi sulla teoria dell’elasticità, sull’integrazione complessa e sul calcolo dei residui.
Nel 1824, alla morte di Luigi XVIII ed alla salita al trono di Carlo X, essendo primo ministro il Villele, inizia una politica di repressione delle società massoniche come la Carboneria e la politica si fa più decisamente più dura. E’ il periodo di massima diffusione delle idee di de Maistre, di de Bonald e del primo Lamennais. In questo periodo, Cauchy è il portavoce all’Accademia delle Scienze del pensiero contro-rivoluzionario, non esitando mai a denunciare la dottrine contrarie alla religione. Si attira così le ire dell’ambiente liberalmassonico universitario. Ad esempio, viene attaccato da Stendhal con critiche maliziose e destituite di ogni fondamento.
Nel 1827 comincia la battaglia a favore della libertà d’insegnamento ed in difesa dei Gesuiti.
Nel 1830, dopo la Rivoluzione di Luglio che spodesta i Borboni, alla salita sul trono del re illegittimo Luigi Filippo d’Orleans, va in volontario esilio in Svizzera, dove avvia il progetto dell’Accademia Elvetica, che avrebbe dovuto accogliere tutti gli scienziati transfughi dalla Francia.
Sempre nel 1830, il Re di Sardegna Carlo Alberto di Savoia (1798-1849) lo chiama a riattivare la cattedra di Fisica Matematica all’università di Torino, che già in precedenze (con il nome di “Fisica Sublime”) fu del famoso e prestigioso Avogadro. Incarico che accetta con entusiasmo tanto da rispolverare in soli tre mesi l’italiano che aveva studiato anni prima per potere tenere i corsi nella lingua degli studenti. Ancora nel 1830, in italiano, scrive “Sui Metodi Analitici” per la Biblioteca Italiana.
Il 15 Gennaio 1832 incontra personalmente Carlo Alberto. Nel marzo del 1832 passa due settimane a Roma ed è ricevuto da Papa Gregorio XVI.
Nel 1833 viene chiamato a Praga da Carlo X di Borbone (1757-1836), anch’egli in esilio, per fare da precettore del nipote, il giovane duca di Borgogna. Bisogna notare, a questo proposito, quale spirito di fedeltà legittimista muovesse Cauchy: uno spirito di tal intensità da far sì che il più grande matematico vivente accettasse di passare il suo tempo ad insegnare le nozioni più elementari della matematica e della fisica ad un alunno che, benché illustre quanto al lignaggio, pare che non brillasse proprio quanto al rendimento … Sembra che spesso facesse perdere la pazienza a Cauchy, che non gli lesinava i rimproveri alzando anche la voce, tanto da far più volte intervenire la regina, la quale, intimorita, gli diceva “… troppo forte, non così forte …”.
E’ comunque in questo periodo di Praga che sviluppa la definizione rigorosa di funzione continua, dopo averne accesamente discusso con il matematico e teologo Bernhard Bolzano (1781-1841).
In considerazione della sua fedeltà, Carlo X lo nomina barone.
Torna in Francia nel 1838, chiamato per riprendere il suo posto di Accademico di Francia, ma rinuncia all’insegnamento perché rifiuta di prestare giuramento al Re Luigi Filippo di Orleans (1773-1850) non riconoscendone la legittimità. Per coerenza personale, il più grande matematico vivente rimane così escluso dall’insegnamento per ben dieci anni. Ancora nel 1838 entra al Bureau des Longitudes, ma anche qui rifiuta di prestare giuramento all’usurpatore, sicché egli agisce come un membro del Bureau, ma non può partecipare alle riunioni delle commissioni direttive. E’ in questo periodo che si occupa di astronomia e di meccanica celeste. Continua la battaglia in difesa dei gesuiti e della libertà di insegnamento.
Nel 1848, il governo repubblicano, nato dalla Rivoluzione di Febbraio, e poi Napoleone III (1808-1873) nel 1852 lo richiamano comunque all’insegnamento, benché Cauchy continui a rifiutare il giuramento.
Il suo atteggiamento e le sue idee cattoliche e legittimiste gli attirano ancora l’ostilità dell’ambiente accademico, ma questo non gli impedisce di diventare una gloria – anzi “la” gloria – della Sorbona.
Nel 1856, mentre è anche uno dei massimi dirigenti della Società di S. Vincenzo de’ Paoli, all’apice della notorietà, fa da relatore della tesi del Beato Francesco Faà di Bruno (1825-1888) che con lui si laurea e diviene il primo matematico cattolico i cui testi vengono adottati nelle facoltà di matematica dell’Inghilterra (come ricorda Vittorio Messori nel suo “Un italiano serio”). Muore nel 1857 per una febbre contratta durante un viaggio. Anche la sua morte fu coerente con la sua fede.
Ecco come la descrive la figlia: ” Essendo rimasto pienamente cosciente, nel pieno possesso delle sue facoltà mentali, fino alle 3.30 del mattino, mio padre improvvisamente sussurrò i nomi benedetti di Gesù, Maria e Giuseppe. Per la prima volta, sembrò prendere coscienza della gravità della sua condizione. Verso le quattro circa, la sua anima tornò a Dio. Andò incontro alla morte con una tale calma che ci fece vergognare del nostro dolore “.
La matematica nel sei/settecento aveva fatto grandi passi in avanti, soprattutto con Eulero, con Legendre, Laplace e Lagrange.
In generale, però, gli studi matematici del Settecento non sono sistematici, ma si basano piuttosto su metodi empirici: “prima dell’introduzione del rigore matematico, l’analisi era un pantheon di falsi dei, e Cauchy, con Gauss ed Abel, li abbatté, facendo opera di grande pioniere” (Bell).
I matematici del secolo dei lumi avevano sviluppato tutte le procedure dell’analisi, il metodo degli infinitesimi, gli sviluppi in serie, il passaggio dai numeri reali a quelli complessi basandosi su ragioni fondate sulla generalità dell’algebra, quasi questa fosse sempre e comunque applicabile. Questa prassi era divenuta un principio metafisico, basato sulla convinzione illuministica dell’infallibilità del pensiero umano. Dal punto di vista del rigore matematico, questo modo di procedere era assolutamente discutibile, tanto che portò spesso a risultati scorretti.
Cauchy, in questo concordando con Lagrange e Laplace, pensava che l’analisi non dovesse essere presentata in modo “semplice” ed esclusivamente orientata alle sue applicazioni ingegneristiche, come invece pretendeva l’Ecole Polytechnique. Pensava che l’analisi dovesse essere sviluppata in modo più generale e più rigoroso, in modo da potersi applicare facilmente ai campi più disparati.
Nel 1816 Von Haller, a proposito della Restaurazione, scriveva: “I Re legittimamente unti hanno riguadagnato i loro troni”. Cauchy pensava che si dovesse sviluppare una scienza “legittima”, di verità universale e di servizio al Signore. Cerchiamo di vedere cosa intendesse.
A proposito della verità, Cauchy affermò: “ La verità è un tesoro inestimabile che, quando riusciamo ad acquisirla, non può portarci rimorso o dolore; non può rendere inquieta o insoddisfatta la nostra anima. Il solo pensiero dei suoi attributi celesti, della sua bellezza divina è sufficiente per ripagarci di tutti i sacrifici che possiamo avere fatto per scoprirla. In realtà, la gioia stessa del paradiso non è nient’altro che il pieno e completo possesso della verità” ed aggiungeva “Qui sulla terra la verità non sarà mai completamente rivelata“.
Cauchy distingueva tra due ordini di verità:
• Verità fiolosofico/morali : le verità proprie della Rivelazione, il cui insegnamento andava lasciato a coloro che egli riteneva a questo deputati: i sacerdoti ed i religiosi.
• Verità scientifiche. Queste erano verità “conquistate”, non rivelate. A questo proposito infatti affermava:
“La ricerca della verità dovrebbe essere l’unico scopo di ogni scienza“.
In questa prospettiva, considerava l’esattezza come la “caratteristica necessaria ed essenziale di ogni scienza“.
Come si vede, quindi, teneva ben distinte la verità fisica da quella metafisica.
In quest’ottica, considerava “esatte” soltanto le scienze che, pur partendo dall’osservazione dei fenomeni naturali passavano poi a darne una codifica matematica esatta, meglio se non basata soltanto sulla statistica.
Considerava le verità scientifiche come soggette a quelle morali e religiose. Invitava quindi la comunità scientifica a respingere quelle teorie che, sotto l’apparenza di verità comunque non comprovabili, contrastavano con le verità rivelate. Le verità fisico/scientifiche sono solo il substrato, il background di quelle scientifiche. E’ questo il motivo, spiegava Cauchy, per cui la Chiesa è assolutamente favorevole al progresso scientifico. D’altra parte, Cauchy riteneva un grave pericolo quello di attribuire valore metafisico alle verità scientifiche, ed affermava: “Il grande crimine dell’ultimo secolo – il settecento, il secolo dei lumi, NDR – è stato quello di voler mettere la natura contro il Creatore e addirittura di armare le scienze contro Dio stesso, le scienze, il cui unico scopo è la ricerca della verità! … Coltiviamo le scienze, ma senza cedere alla tentazione di estenderle oltre i propri confini . Non pensiamo di poter trattare la storia in termini di formule, e non cerchiamo di basare la morale su teoremi di algebra o di calcolo integrale …”
Ecco uno schema interpetativo della conoscenza secondo Cauchy:
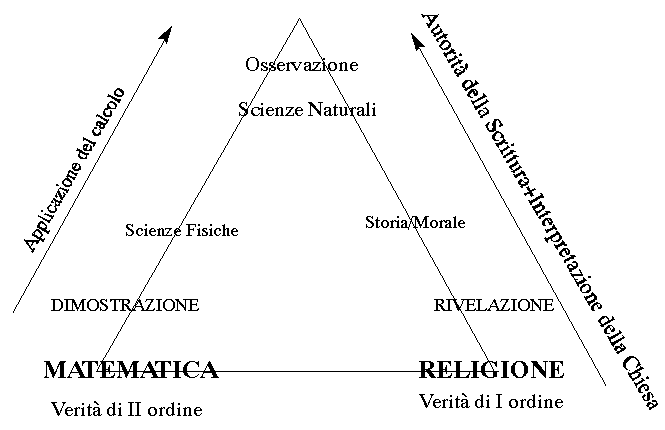
E’ da queste convinzioni che nasce l’idea del rigore matematico. Infatti, è solo grazie al rigore ed alla corretta e chiara definizione del suo campo di validità – quindi dei suoi limiti – che la matematica può essere sottratta a quella prassi illuministica che ne faceva una verità metafisica e quindi ne estendeva indebitamente i risultati, giungendo spesso a conclusioni erronee.
E’ proprio in questo campo che interverrà Cauchy, introducendo un rigore assolutamente sconosciuto fino a quel momento. E, come abbiamo cercato di mostrare, non è affatto casuale che questa importantissima svolta nel pensiero matematico sia dovuta ad uno scienziato cattolico e contro-rivoluzionario. E’ anzi proprio in virtù delle sue convinzioni che egli sviluppò quell’architettura di esattezza e precisione che è alla base della moderna analisi..
La matematica moderna deve quindi a Cauchy molte importantissime innovazioni, ognuna delle quali segna una svolta sulla via seguita dalla matematica del Settecento, tra cui l’introduzione dell’esattezza nell’analisi matematica e l’apporto fondamentale dell’analisi combinatoria. Cauchy, dunque, stabilisce il calcolo differenziale ed integrale su solide basi. Egli è il codificatore della matematica moderna per eccellenza, il matematico a cui si devono la sistematicità, l’eleganza della forma ed il rigore delle dimostrazioni.
E’ importante notare che su questo punto concordano sia gli studiosi di tendenza illuminista/razionalista, come il Bell ed il Boyer, che quelli di formazione rigorosamente cattolica, come Gianfranco Basti (a testimonianza del fatto che, nonostante la tronfia prosopopea illuministico razionalista, l’azione più importante a favore del rigore e dell’esattezza matematica – azione di una portata veramente stravolgente, vorrei usare il termine rivoluzionario, se non lo detestassi – , vengano proprio dal reazionario, bigotto, monarchico Cauchy).
Ecco la moderna definizione di limite (1821), codificata così come la propose Cauchy:
Quando i valori successivamente attribuiti ad una variabile si avvicinano indefinitamente ad un valore fisso in modo tale da differire da esso di una quantità tanto piccola quanto si vuole, allora quel valore fisso è detto il limite di tutti gli altri.
Ed eccola tradotto nel linguaggio più attuale “delta-epsilon” (la precedente definizione, molto più imprecisa, era di D’Alembert – Jean Baptiste Le Rond D’Alembert,1717-1783, famoso enciclopedista, redattore di tutte le voci di matematica dell’enciclopedia):

Analogamente, definì gli infinitesimi :
Quando i valori successivi della medesima variabile diminuiscono indefinitamente, così da diventare più piccoli di qualsiasi numero prefissato, questa variabile diviene quel che si dice un infinitesimo o una quantità infinitamente piccola. Una siffatta variabile ha zero come limite.
Questa definizione di infinitesimo è importantissima proprio perché mentre i matematici precedenti avevano concepito un infinitesimo come numero fisso molto piccolo, Cauchy lo definisce chiaramente come una variabile dipendente.
Dalla definizione di limite deriva anche la nozione di funzione tendente all’infinito:
Una quantità infinità e quella data da una variabile i cui valori numerici aumentano continuamente, in modo tale da divenire più grandi di qualsiasi numero predefinito.
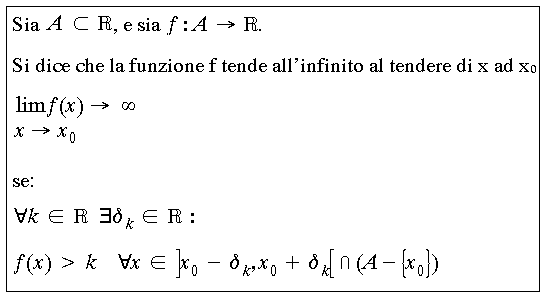
Con riferimento a quanto disse molto opportunamente l’amico prof. Gallotta in una lezione del corso dell’anno precedente, è vero che questa definizione di “infinito” si presta ad interpretazioni di stampo relativistico e quindi riduttivo del significato flisofico-metafisico del concetto di infinito. Ma è d’altra parte altrettanto evidente che con una definizione così rigorosa come quella proposta in base alle enunciazioni di Cauchy, l‘ambito della definizione è immediatamente chiarito e ben delimitato. Con il rigore introdotto, l’infinito di cui si parla non può essere confuso con concetti metafisici. Qui si parla soltanto di relazioni fra numeri.
A proposito delle serie numeriche e di potenze, Cauchy dice una parola definitiva, sviluppando una teoria coerente e rigorosa – sono famosi i suoi “criteri di convergenza” -, laddove nel Settecento non esisteva alcuno studio sistematico ed addirittura il famoso Leonardo Eulero (1707-1783; svizzero, famosissimo allievo dei Bernoulli, professore sia in Prussia che a Pietroburgo; autore di una vastissima produzione; si ricordino ad esempio i “diagrammi” di Eulero-Venn, con i quali ancora si mostrano gli insiemi) parlava – con linguaggio invero poco rigoroso – di “serie più o meno convergenti”!
Ecco il principale criterio di convergenza di Cauchy:
Perché la serie u0, u1, u2, …, un, un+1 sia convergente, … è necessario che per valori crescenti di n, … la somma delle quantità un, un+1, un+2, … prese dalla prima, in numero qualsiasi, finisca per assumere costantemente valori numerici che sono inferiori a qualsiasi limite dato. Viceversa, quando queste diverse condizioni sono soddisfatte, la convergenza delle serie è garantita.
In realtà il viceversa non è vero, come mostrò Abel in un celebre controesempio.
Cauchy diede anche una fondamentale e rigorosa definizione delle funzioni continue (dopo accese ma illuminanti discussioni con Bolzano a Praga):
Sia f(x) una funzione della variabile x e si supponga che, per ogni valore di x compreso tra due valori estremi dati, questa funzione prenda costantemente un valore finito. Se, per un valore di x compreso fra gli estremi dati, si attribuisce un incremento a infinitamente piccolo, la funzione sarà incrementata della seguente differenza:
f(x + a) – f(x)
che dipenderà allo stesso tempo dalla nuova variabile e dal valore di x. Ciò premesso f(x) sarà una funzione continua della variabile x tra gli estremi dati, se , per ciascun valore di x compreso fra tali estremi, il valore numerico della differenza f(x + a) – f(x) diminuisce indefinitamente assieme ad a. In altre parole, la funzione f(x) rimane continua tra due estremi dati, se tra tali estremi, un incremento infinitamente piccolo della variabile produce sempre un incremento infinitamente piccolo per la funzione stessa.
Ed ecco la codifica moderna, in termini “delta-epsilon”, del medesimo concetto.

e cioè:
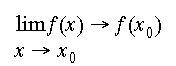
Si dice più semplicemente che l’immagine inversa di ogni insieme aperto (nel codominio) tramite la funzione è un aperto (nel dominio):
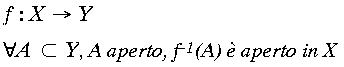
Si pensi al grande passo in avanti che questa definizione produce: la definizione precedente, data da Eulero, denominava continue soltanto le funzioni definite da una singola espressione analitica.
Il concetto di continuità è essenziale per la soluzione di un enorme numero di questioni di matematica. Ma è anche essenziale nelle sue applicazioni alla fisica ed all’ingegneria. Si pensi ad esempio che i punti in cui una funzione (quindi una curva, una superficie) è continua sono quei punti in cui uno strumento per la lavorazione a Controllo Numerico potrà eseguire la lavorazione stessa senza problemi, mentre i punti in cui la funzione non è continua sono quelli in cui bisognerà ricorrere ad accorgimenti particolari. Ancora, in forma impropria, ma suggestiva, si può dire che una funzione è continua quando il suo grafico può essere disegnato “senza staccare la penna dal foglio“.
Del 1823 è la definizione di derivata in un punto come limite del rapporto incrementale al tendere a zero dell’incremento . Si pensi che la definizione precedente, di Lagrange, definiva la derivata in modo davvero poco rigoroso come il secondo termine dello sviluppo in serie di Taylor.
Segue poi la definizione di integrale come limite di una somma . Dato l’intervallo [x0, X], l’integrale della funzione f su tale intervallo e’ il limite della seguente somma, al tendere all’infinito delle suddivisioni dell’intervallo:
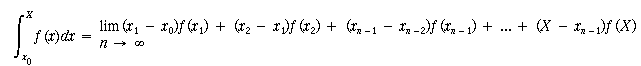
L’originalità di questa definizione sta tutta nell’avere svincolato l’integrazione dalla sua subordinazione alla derivazione: l’integrale non è più concepito come operazione inversa della derivata, come “antiderivata”, ma come processo a sé stante.
Ancora, per tutto il Settecento le ricerche sulle equazioni differenziali sono dirette alle applicazioni ed alla ricerca esplicita delle soluzioni di caso in caso. E’ soltanto Cauchy che sviluppa una teoria sistematica, dimostrando l’esistenza e l’unicità della soluzione per le equazioni differenziali lineari data una condizione iniziale (il famosissimo “Problema di Cauchy”).

Il problema di Cauchy trova innumerevoli applicazioni in meccanica ed elettricità. Legato al problema di Cauchy è anche il teorema fondamentale del calcolo integrale, che in un certo senso ne è un formulazione diversa, che stabilisce in modo rigoroso che la derivata della primitiva di una funzione, con le suddette condizioni, è la funzione stessa.
Per restare nel campo dell’analisi, occorre citare che Cauchy provò anche la formula del resto nella forma di Taylor e Mac Laurin, quella di Lagrange ed anche una forma nuova, detta appunto di Cauchy.
I contributi specifici di Cauchy spaziano quindi dal concetto di limite e dagli studi rigorosissimi sulle funzioni continue, alla derivazione, all’integrazione, alle basi della modernissima teoria dei gruppi . Tale teoria elementare, ma tutt’altro che semplice, scaturisce da un modo nuovo ed originale di riguardare l’algebra, intuendo il legame, il filo conduttore che sta sotto le formule e la loro simmetrica armonia, scorgendovi il concetto generale di operazione e le leggi che ne consentono la combinazione. Questa teoria è inoltre di importanza capitale nella matematica moderna: si applica alle equazioni algebriche, alla geometria dei cristalli, allo studio della struttura atomica ed alla moderna elaborazione delle equazioni differenziali. Cauchy giunse a porre le basi della teoria dei gruppi partendo dalle permutazioni, o meglio dalla teoria delle sostituzioni, che elaborò attorno al 1840, dalla quale scaturirà la teoria dei gruppi finiti. Grazie a questa teoria, circa vent’anni più tardi il matematico Evariste Galois riuscirà a determinare soluzioni per le equazioni di grado superiore al quarto.
Cauchy studiò, cercando di astrattizzarle, le “operazioni”. Vediamo come procedette. Indichiamo le operazioni con lettere maiuscole: A, B, C eccetera. AB significa che l’operazione A viene eseguita prima dell’operazione B. Perciò AB non è necessariamente uguale a BA. Cauchy stabilì che un insieme di operazioni formano un gruppo se:
- Esiste una regola applicabile ad una qualunque coppia di operazioni dell’insieme tale che la operazione risultante faccia ancora parte dell’insieme
- La regola di cui in 1) è associativa: A(BC)=(AB)C
- Esiste un’operazione I nell’insieme dato tale che per ogni operazione A dell’insieme: AI=IA=A (I è detta identità)
- Per ogni operazione dell’insieme esiste l’operazione inversa. AA’=I.
La teoria dei gruppi (vedi il gruppo delle curve ellittiche) è anche alla base della moderna crittografia: la stessa che ha assunto la massima importanza durante l’ultimo conflitto mondiale ed ha impegnato fior di matematici sia dell’Asse che di parte alleata. Probabilmente, per lo scalpore che ha suscitato, ricorderete la recente dimostrazione del teorema di Fermat (“Non esiste alcun numero intero n>2 tale che xn+ yn = zn“), che ha richiesto più di 300 anni: anche questa si basa sulla teoria dei gruppi e sfrutta un gruppo che lo stesso Cauchy riconobbe come tale: il gruppo delle curve ellittiche (una curva ellittica è un insieme di punti che soddisfanno alla seguente equazione: y2 = x3+ax+b, dove a, b, x ed y sono numeri reali). Anche Cauchy tentò una soluzione per il Teorema di Fermat: vi giunse molto vicino, ma non l’ottenne. Senza i suoi studi, però, quest’annosa questione non avrebbe mai potuto essere risolta. Non è questa la sede per esposizioni di carattere tecnico, ma un cenno per capire la portata di ciò di cui stiamo parlando lo si può dare. Ecco la definizione di gruppo:
“Sia dato un insieme G ed una regola (legge di composizione – cioè una OPERAZIONE) di composizione fra i suoi elementi che indicheremo con +. L’insieme G si dice gruppo rispetto all’operazione + se:
- G è chiuso rispetto a +. Cioè se: per ogni x ed y appartenenti a G, x+y appartiene a G
- Comunque si prendano x, y e z in G: (x+y)+z=x+(y+z)
- In G esiste un elemento, che chiameremo 0, tale che: x+0 = 0+x = x per ogni x di G.”
Ad esempio, i numeri interi relativi Z costituiscono un gruppo rispetto all’operazione di addizione.
E ancora Cauchy si occupò brillantemente di analisi complessa, un campo in cui fu fondatore ed esploratore, particolarmente con lo studio delle funzioni di una variabile complessa e con la teoria dei residui (con il suo studente amico russo Ostrogradski), con gli integrali singolari e con la famosa integrazione lungo un percorso chiuso. Diede anche il suo contributo alla teoria delle trasformate di Fourier.
Si occupò anche di fisica, con la teoria delle onde e gli studi di ottica. Importantissima è la sua teoria dell’elasticità, nella quale generalizzò i risultati di Hooke.
In meccanica dei fluidi, approfondì gli studi di Navier e di Laplace, mentre per l’elaborazione della teoria della luce fu in contatto con Fresnel e diede un contributo importante introducendo i metodi dell’analisi.
Si occupò anche di astronomia, studiando le opere di Urbain Le Verrier (1811-1877) sull’asteroide Pallade e diede un contributo fondamentale dimostrando un metodo che consentiva di eseguire i calcoli astronomici ad una velocità strabiliante.
Fu il primo a dare una dimostrazione rigorosa del “teorema di Taylor” (che deve il suo nome al matematico inglese Brook Taylor, 1685-1731). Le sue scoperte matematiche troveranno applicazioni utilissime anche nel campo dell’elettromagnetismo. Nei corsi universitari di Analisi Matematica il suo nome ricorre un numero elevatissimo di volte. La sua produzione scientifica comprende circa 800 memorie e molte opere didattiche, fra le quali:
- “Cours d’analyse de l’Ecole royale polytechnique” (1821)
- “Résumé des leçons données à l’Ecole royale polytechnique sur les applications du calcul infinitésimal” (1823)
- “Leçons sur les applications du calcul infintésimal à la géométrie” (1826, 1828)
- “Leçons sur le calcul différentiel” (1829)
- “Anciens exercices de mathématicques” (1826-1830)
- “Résumés analytiques” (1833)
- “Noveaux exercices de mathématiques” (1835-1836)
- “Noveaux exercices d’analyse et de physique mathématique” (1840-47).
L’ultimo biografo (in senso cronologico), Belhoste, esprime sulla figura di scienziato di Cauchy il seguente giudizio:
“… una tale creatività scientifica è niente di meno che sbalorditiva, perché presenta la ricerca in tutte le aree allora conosciute della matematica. Nonostante la sua vastità ed il suo carattere poliedrico e dalle molte sfaccettature, il lavoro scientifico di Cauchy possiede un tema unificatore di fondo, una sua integralità segreta. … Il genio creativo di Cauchy trovò larga espressione non solo nel suo lavoro sulle fondamenta dell’analisi reale e complessa, aree alle quali il suo nome è inscindibilmente connesso, ma anche in altri campi. Specificamente, …, bisogna menzionare i suoi grandi contributi allo sviluppo della fisica matematica e della meccanica teorica: ad esempio le sue due teorie dell’elasticità e le sue ricerche sulla teoria della luce, che richiedettero che egli sviluppasse tecniche matematiche nuove, come le trasformate di Fourier, la diagonalizzazione delle matrici ed il calcolo dei residui. ”
Nella sua vita, Cauchy è un esempio di intellettuale cattolico, ma anche di cattolico consapevole nell’impegno politico e sociale, fedele al Re ed attivo nelle opere di carità.
Cauchy, per tutta la vita, subì gli attacchi dell’ambiente anticattolico del suo tempo. Ma questo non lo scoraggiò dalla sua principale occupazione extraprofessionale: la carità. Quando non era impegnato in qualche problema matematico, lavorava a qualche nuova missione di pietà per i meno fortunati.
Come si è detto, nel 1808 entra a far parte della Congregazione della Santa Vergine , (Congregation de la Saint Vierge), fondata nel 1801 dal gesuita padre Jean-Baptiste Bourdier Delpuis, allo scopo di riunire i giovani di buona famiglia in preghiera comunitaria e unirli contro le minacce rappresentate dalla mancanza di fede, miscredenza, irreligione e secolarismo di quei tempi. Lo scopo della congregazione, il cui motto era cor unum et anima una era quello di formare una elite di giovani cattolici che andasse ad occupare posti influenti nel mondo della scienza e della politica, allo scopo di ricostruire l’intelaiatura cattolica della società, assolutamente perduta e caduta in mani nemiche con il secolo dei lumi e la Rivoluzione. In seguito, questa organizzazione cattolica contro-rivoluzionaria si occuperà di dare vita ad un insieme di associazioni ed organismi che andranno ad operare nel sociale con scopi caritativi mirati e particolari (la S. Vincenzo nascerà come continuazione/emanazione della società della S. Vergine). Nel 1816 Cauchy è incaricato di organizzare la Società delle Buone Opere , con il triplice scopo di:
- Visitare i malati negli ospedali
- Visitare i detenuti nelle prigioni
- Insegnare il catechismo agli spazzacamini
A questa organizzazione lavorerà instancabilmente, assieme a figure di contro-rivoluzionari come Lamennais, Matthieu de Montmercy e Alexis de Noailles.
Più tardi lavorerà con la Società Cattolica dei buoni Libri, per la diffusione a basso prezzo della stampa cattolica. Di questa associazione sarà, con il duca di Montmercy, uno dei direttori. Fra le intenzioni della S. Cattolica dei Buoni Libri vi era quella di pubblicare un’enciclopedia cattolica contro-rivoluzionaria, ma questo progetto venne ostacolato dalla potente corrente Gallicana della chiesa francese, capeggiata dall’Abbè Clausel.
Cauchy fu poi coinvolto in prima persona nella battaglia per la libertà di educazione che si svolse tra i Gesuiti e l’Università, dalla parte dei primi e contro il monopolio statale della seconda. Nel 1827 si espose particolarmente a favore della libertà di educazione, sostenendo apertamente le Scuole dei Fratelli Cristiani di Bretagna.
In questi anni, si verifica una strana alleanza, una sorta di tacito accordo, tra liberali e gallicani, che attaccano da due fronti i Gesuiti, ingiustamente accusati di un complotto clericale per l’instaurazione della teocrazia. La propaggine laica della Società di Gesù era la Società della Santa Vergine, di cui Cauchy era uno dei dirigenti. In questo clima, per timore di rivalse, il re sente la necessità di fare concessioni ai liberali ed ai gallicani, sottoponendo tutte le scuole le scuole della chiesa al controllo dell’università ed impedendo l’insegnamento ai Gesuiti. Come reazione, con altre 44 persone, fra cui gli amici Ampere e Binet, Cauchy fondò l’Associazione per la difesa della Religione Cattolica, con lo scopo di difendere i diritti della Chiesa e di diffondere idee contro-rivoluzionarie. Con Ampere e Binet, terranno corsi per gli studenti delle scuole dei Gesuiti che erano state chiuse. E’ di questo periodo il voltafaccia di Lamennais, che, essendo dapprima su posizioni molto più “teocratiche” di quelle degli altri contro-rivoluzionari (che invece erano più vicini a de Maistre e de Bonald) ritenne troppo “timide” le reazioni di questi ultimi. Per reazione, si diceva, abbraccerà il cattolicesimo liberale (analogamente a quanto succederà più tardi in Italia ai più “duri e puri” fra gli intransigenti dell’Opera dei Congressi).
Poco prima della rivoluzione del luglio 1830, quando Laffitte, Thiere e La Fayette sostenendo il duca di Orleans spodesteranno Carlo X (che andrà in esilio abdicando a favore del nipote duca di Bordeaux), Cauchy si era reso autore di un famoso atto di coraggio, per avere pubblicamente strappato la lista dei candidati liberali alle elezioni universitarie.
Come si è detto, alla salita al potere dell’usurpatore Luigi Filippo d’Orleans, Cauchy rifiuta il giuramento di fedeltà e quindi:
- il 26 Novembre 1830 viene destituito da professore alla facoltà di Scienze
- Nel Febbraio 1831 viene estromesso dalla Ecole Polytecnique
- In Marzo dello stesso anno viene espulso come ingegnere dalla società des Pont et Chausses
Con ogni probabilità, nel luglio 1830 nasconde in casa propria alcuni Gesuiti in fuga dalle purghe liberali e li accompagna personalmente ed a proprio rischio in Svizzera. La sua battaglia per i gesuiti e la libertà d’insegnamento continua negli anni. E’ in contatto con l’Abbè Moigno, incaricato dell’istruzione matematica dei Gesuiti e da lui designato suo sostituto a Torino nella cattedra di Fisica Matematica quando andrà a fare da precettore al duca di Bordeaux.
Nel 1839, mentre prestava il suo aiuto alla Scuola Normale Ecclesiastica, fu tra i fondatori dell’Institute Catholique, con lo scopo di tenere corsi di filosofia, lettere e scienze per sopperire alla mancanza di un’università cattolica. Cauchy dirige il comitato scientifico dell’Institue Catholique, del quale chiama a far parte gli scienziati contro-rivoluzionari Coriolis, Binet, Freycinet, Beudant ed altri.
Quasi contemporaneamente, cominciano ad organizzarsi anche i cattolici liberali di Ambroise Rendu nel Cercle Catholique, che si mette da subito in concorrenza con l’Institute catholique, forte dell’appoggio del famoso letterato Ozanam, capofila dei cattolici liberali.
In questo periodo, anche nelle nuove organizzazioni di carità la coesistenza tra cattolici contro-rivoluzionari e cattolici liberali non è semplice. La società di Saint-Vencent de Paul, intanto, prende gradualmente il posto della Società della Santa Vergine.
Ricopre la carica di dirigente della società di San Vincenzo de’ Paoli svolgendovi un’intensa attività a favore dei poveri e fonda le Conferenze di Sceaux, con lo scopo di aiutare gli indigenti.
Nell’aprile del 1839, Monsignor Gilis, Vescovo di Edinburgo, fonda la società Cattolicesimo in Europa , per aiutare i cattolici vessati in varie parti dell’Europa protestante-anglicana e soprattutto in Scozia, Inghilterra ed Irlanda. Cauchy aderisce fin dal primo momento, riuscendo a raccogliere l’adesione di 40 vescovi e di 1200 importanti sottoscrittori, ma incontrando fin da subito l’ostilità dei cattolici liberali.
Nel 1843 fonda il Comitato di Difesa della Libertà di Insegnamento , grazie al quale i gesuiti attaccano con molta decisione il monopolio statale sulle università.
In quegli anni, ancora a causa del rifiuto di prestare giuramento all’usurpatore ed dell’inasprimento della politica massonico-liberale, perde il posto al Collegio di Francia ed anche al Bureau des Longitudes.
Fra le sue amicizie più intime vi è il famoso predicatore gesuita Padre Gustave Xavier Lacroix de Ravignan (1795-1858), noto per le sue omelie in Nôtre Dame incentrate soprattutto sul conflitto tra verità ed errore e per essere il più combattivo fra i Gesuiti a difesa della Compagnia.
Cauchy si espone personalmente scrivendo due memorie in difesa della Compagnia di Gesù quando questa, durante il regno di Luigi Filippo, diviene oggetto di violentissimi attacchi: “Considerazioni sugli ordini religiosi indirizzati agli amici delle Scienze” (marzo 1844) e “Memoria indirizzata ai membri delle due camere”. Ancora nel 1844 pubblica “Riflessioni sulla libertà d’insegnamento”, in cui riafferma la necessità dell’istruzione religiosa e condanna il cattolicesimo liberale di Lamennais e si scaglia ancora contro il monopolio statale dell’università. Purtroppo, nel 1844, le istituzioni dei Gesuiti vengono chiuse in Francia, e la Compagnia sciolta, con il beneplacito di papa Gregorio XVI.
Nel frattempo, continua ad occuparsi di opere di carità. Con abili mosse diplomatiche, riesce quasi sempre ad ottenere improbabili approvazioni e finanziamenti dai suoi conoscenti dell’Accademia delle Scienze (da cui, ricordo, era stato espulso). E’ proprio nel 1844 che dà vita alla Societe de Saint-Regis, organizzazione che cerca di ottenere il matrimonio civile e religioso per le coppie conviventi irregolari e le legittimazione dei loro figli. Cauchy si impegna per ottenere forti vantaggi fiscali per tali coppie, spesso in tali condizioni di miseria da non potere sostenere le onerose tassazioni matrimoniali imposte dal governo liberal-massonico.
Nel 1846, in occasione della grande carestia dell’Irlanda, rivolge al Papa un accorato appello a favore di quella popolazione colpita dalla fame e dalla carestia, ma anche dalla vessazione dell’Inghilterra protestante.
Si occupa anche delle prigioni, chiedendone la riforma, con lo studio “Considerazioni sui metodi di prevenzione del crimine e di rieducazione dei criminali“.
E’ tra i fondatori della “Association pour la liberté du dimanche ” sorta per favorire l’abolizione del lavoro festivo, al fine di consentire il riposo domenicale anche agli strati meno abbienti della popolazione.
La sua attività si svolge anche fuori dalla Francia e Cauchy ha un ruolo fondamentale, in occasione della guerra di Crimea (1856-1856) nella creazione delle “Ecoles d’Orient “, con lo scopo di diffondere il Vangelo fra le popolazioni musulmane. L’aspetto religioso ha sempre avuto, per lui, eminente scienziato, la priorità su quello scientifico, tanto che quando il famoso fisico William Thomson (Lord Kelvin, 1824-1907) seguace della Chiesa Libera Scozzese lo visita per discutere di matematica, Cauchy impiega tutto il tempo per cercare di convertirlo al cattolicesimo.
4. Il dileggio
A causa della sua devozione e dell’integralità della sua adesione alla fede Cattolica e delle sue convinzioni legittimiste, su Cauchy si abbate il sarcasmo di molti degli autori che si sono occupati di Lui: viene spesso talmente dileggiato, chiamato bigotto, Don Chisciotte (Bell), ed altro ancora, che risulta difficile farsene un’idea equilibrata.
Da tutti traspare il fastidio di dover occuparsi di un personaggio di così alto profilo dal punto di vista scientifico, tanto da non poter assolutamente essere trascurato, ma “viziato” dal suo cattolicesimo integrale, quasi si trattasse di una colpa: e forse proprio di questo si tratta, in un ambito in cui la citata “vulgata scientista”, razionalista non può tollerare, con l’illiberalità che le è propria, il debito che il mondo matematico moderno ha nei confronti della nobile figura di Cauchy.
I biografi razionalisti sono tutti concordi nel sottolineare che era bigotto, intrattabile, maniaco religioso, ecc. E si parla di uno dei più grandi matematici di tutti i tempi. Quando si parla di altri, di diversa tendenza, non si trova ovviamente lo stesso atteggiamento. Ad esempio se si parla di Carnot (famoso soprattutto per l’omonimo teorema sui triangoli), si tace un piccolo insignificante particolare, e cioè che fu uno dei mandanti e degli organizzatori del genocidio vandeano …
Si perpetuano nella letteratura l’astio, la malsopportazione ed il dileggio che per quasi tutta la vita Louis Augustin Cauchy dovette sopportare (e talora a fatica, dando anche segni d’insofferenza, ma sempre con lo sguardo rivolto verso la meta) da parte di un ambiente rivoluzionario e radicalmente contrario al suo modo non solo di pensare, ma anche di essere.
Ad esempio, Niels Henrik Abel (1802-1829), il famoso matematico norvegese figlio di un pastore protestante che per lungo tempo soggiornò a Parigi disse di lui: “Cauchy è bigotto, cosa strana in uno scienziato”.
Colerus (storico razionalista della matematica): “Cauchy aveva un carattere spesso poco in armonia con le opere e andava soggetto a frequenti attacchi di invidia e di cattiveria …” , mentre abbiamo già mostrato, tramite le sue opere, quale fosse la “cattiveria” di Cauchy.
Anche nei due recenti testi sul teorema di Fermat il giudizio che viene dato di Cauchy è veramente inaccettabile: si tratta di un pre -giudizio, basato su quale vulgata razionalista/illuminista che mi sono sforzato di smentire.
A dispetto delle prove, infatti, Cauchy riuscì sempre a destreggiarsi, e a volte perfino a convertire alcuni di coloro che lo dileggiavano e lo prendevano di mira.
5. Conclusioni
Il mondo intellettuale scientista e razionalista mal sopporta lo scienziato che testimonia il legame profondo tra Fede Cristiana e progresso scientifico, consapevole che è grazie alla visione cristiana unitaria del creato che l’indagine scientifica può assumere quel carattere di organicità che è indispensabile per la corretta comprensione dei fenomeni naturali.
Cauchy è un uomo che ha preso sul serio i Comandamenti, pagando duramente di persona, e che si è sforzato di osservarli e di metterli in pratica nel privato e nel pubblico, sul lavoro ed in politica. Poco prima di morire, pronunciò la famosa frase: “Gli uomini muoiono, ma le loro opere rimangono”. E le opere di cui parlava non erano certamente soltanto quelle di matematica.
“La fede e la ragione sono come le due ali con le quali lo spirito umano s’innalza verso la verità. È Dio ad aver posto nel cuore dell’uomo il desiderio di conoscere la verità e in definitiva, di conoscere Lui perché, conoscendolo e amandolo, possa giungere anche alla piena verità su se stesso (cfr Es 33,18; Sal 27[26],8-9; 63[62],2-3; Gv 14,8; 1 Gv3,2)” (Fides et ratio: Lettera Enciclica del Sommo Pontefice Giovanni Paolo II ai Vescovi della Chiesa Cattolica circa i rapporti tra fede e ragione, Libreria Editrice Vaticana, Roma 1998; pag. 1): queste stesse parole del Sommo Pontefice Giovanni Paolo II potrebbero applicarsi a Cauchy, descrivendone completamente la figura di scienziato e di uomo.
Quando Gustave Eiffel (1832-1923) costruì la torre parigina che da lui prende il nome, incluse il nome di 72 scienziati francesi nelle placche circostanti il primo livello: fra questi anche quello di Augustin Louis Cauchy. Ma la sua vera gloria è quella di essere morto pronunciando come ultima parola il nome di Gesù, per la testimonianza del quale, anche come scienziato, aveva speso generosamente la vita.
Bibliografia completa utilizzata
0. B. Belhoste, Augustin-Louis Cauchy. A Biography (New York, 1991).
1. Dalla voce Augustin-Louis Cauchy, in “The Catholic Encyclopedia”, copyright © 1913 by the REncyclopedia press, Inc. Electronic version copyright © 1996 by New Advent, Inc.
2. E.T. Bell, I grandi matematici (tit. orig.: Men of Mathematics), Sansoni, Firenze 1973, pag. 274.
3. Igor Safarevic, Il socialismo come fenomeno storico mondiale, Cooperativa editoriale ‘La Casa di Matriona’, Milano 1980
4. Carl B. Boyer, Storia della matematica (tit. orig.: A history of Mathematics), Oscar Mondadori, Arnoldo Mondadori Editore, Milano 1997
5. M. T. Borgato – L. Pepe, Note Critiche di Analisi Matematica, Editrice Universitaria, Ferrara 1979
6. Gianfranco Basti, Il rapporto mente-corpo nella filosofia e nella scienza , PDUL Edizioni Studio Domenicano, Bologna 1991, pag. 204.
7. Vittorio Messori, Un italiano serio: il beato Francesco Faà di Bruno, Edizioni Paoline, Cinisello Balsamo (Milano), pag. 70.
8. http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/cauchy.html
(School of Mathematical and Computational Sciences at the University of St. Andrews, UK. MacTutor History of Mathematics Archive, Index of /~history/Mathematicians: Augustin Louis Cauchy).
9. Enrico Giusti, Analisi Matematica, volume secondo, Libreria Scientifica Giordano Pellegrini, Pisa-1980
10. W.V. Quine, I fondamenti della matematica, SCIENTIFIC AMERICAN, Settembre 1964, in “Verità e Dimostrazione – Questioni di matematica. Presentazione di Carlo Ciliberto” – Letture da LE SCIENZE edizione italiana di SCIENTIFIC AMERICAN, Milano 1978.
11. Egmont Colerus “Piccola storia della matematica da Pitagora a Hilbert”, Einaudi, 1938
12. Simon Singh, L’ultimo teorema di Fermat, Rizzoli RCS Libri, Milano agosto 1997
13. Amir D. Aczel, L’enigma di Fermat, Il Saggiatore, Milano 1998